
Ce premier article doit être lu comme une introduction aux problématiques liées à la génération de contenu aléatoire. Il présente rapidement l’usage récurrent de l’aléatoire dans notre quotidien, des exemples de défauts d’implémentation connus et les outils aujourd’hui disponibles pour tenter de qualifier les sorties aléatoires.
Un second article prévu pour novembre 2023, évoquera plus en détail les tests statistiques pouvant être utilisés, une proposition de procédure d’audit statique et dynamique sur ce type d’algorithmes et d’implémentations, ainsi que de l’outillage adapté pour une approche d’audit en vue d’identifier des biais sur des générations aléatoires.
Ainsi, dans ce premier article, nous présentons tout d’abord les enjeux et les besoins auxquels répond la génération de nombres aléatoires.
Dans un second temps, nous étudions quelques vulnérabilités dues à la conception de certains générateurs aléatoires, dans le but de rappeler la nécessité de contrôler la qualité de leur implémentation.
Enfin, nous proposons un état des lieux des outils open source actuellement disponibles et permettant de qualifier la sortie de générateurs aléatoires.
La rédaction de cette série de deux articles sur les générateurs de nombres aléatoires a été réalisée à la suite de prestations d’audits de générateurs de nombre aléatoire effectuées par XMCO, notamment dans le cadre d’audit d’Homologation ANJ (Autorité Nationale des Jeux).
L’aléatoire en pratique : usage et enjeux
En cryptographie, la génération de nombres aléatoires de grande qualité est fondamentale pour garantir la sécurité des communications et des transactions en ligne. C’est le caractère imprédictible de ces nombres qui rendent les secrets, clés ou autres moyens de chiffrement impossibles (ou du moins très difficiles) à attaquer.
Sachant que des usages aussi courants que le simple envoi d’un courriel, la connexion à un site de commerce en ligne ou encore l’achat de billets de train nécessitent l’utilisation de notions de cryptographie afin d’en garantir la sécurité, s’assurer de la qualité des nombres aléatoires utilisés est fondamental.
Concrètement, les processus suivants requièrent tous la génération de séquences aléatoires :
- Génération de mots de passe
- Génération de clés publique / privée
- Initialisation des connexions sécurisées via SSL / TLS
- Génération de jetons de session
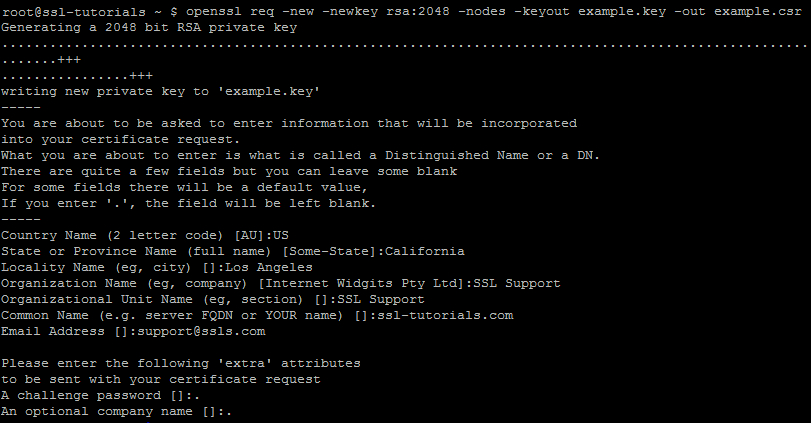
Par exemple, OpenSSL utilise des générateurs de nombres aléatoires lors de la génération de certificats SSL/TLS. Plus précisément, l’utilisation de l’aléatoire est faite pendant la génération des clés cryptographiques, telle que les clés RSA (les …..+++ sur l’image ci-dessous), pour garantir l’imprédictibilité des paramètres cryptographiques associés à cette clé.
Un mécanisme de génération de nombres aléatoires de bonne qualité est également requis dans les programmes et services fournissant des jeux d’argents : poker en ligne, prise de paris, machines à sous virtuelles…
Dans ce cas-là l’enjeu financier requiert évidemment une imprévisibilité parfaite de l’aléa.
En restant dans le domaine du divertissement, les jeux-vidéos utilisent également l’aléatoire afin d’obtenir une certaine imprévisibilité dans le comportement des personnages ou encore dans la génération d’évènements ou de niveaux. Cette mécanique permet d’améliorer la durée de vie des jeux en question.
Par exemple, dans le tout récent jeu d’exploration spatiale « Starfield », une partie des planètes que le joueur peut explorer sont générées procéduralement [STAR] : une partie des éléments du décor sont décidés et rendus aléatoirement.

Par ailleurs le modèle économique de nombreux jeux-vidéos modernes repose parfois sur l’achat de coffre à butin (lootbox), dont le contenu est également généré aléatoirement. On remarquera d’ailleurs que, bien que plusieurs pays comme les Pays-Bas ou la Belgique aient requalifié ce système en jeu d’argent, ce n’est toujours pas le cas en France [MONDE]. Les éditeurs de jeux-vidéos échappent ainsi à la régulation de l’ANJ qui impose des normes précises qui peuvent contraindre l’implémentation.
En outre, dans les simulations numériques et modèles probabilistes, l’incorporation de l’aléatoire dans les calculs permet de prendre en compte les incertitudes et variations inhérentes aux modèles étudiés. Dans des domaines aussi divers que la météorologie, la physique des particules, la finance ou encore la résistance des matériaux, on utilise des modèles statistiques nécessitant des nombres aléatoires pour créer des modèles précis et efficaces.
Par exemple, la méthode de Monte-Carlo [MC] utilise des procédés d’échantillonnage aléatoire pour calculer des intégrales parfois très complexes.
Dans le domaine de l’intelligence artificielle, la plupart des modèles d’apprentissage utilisent également des générateurs de nombres aléatoires dans leurs algorithmes. Par exemple, il est possible d’entrainer des arbres de décision à détecter les intrusions sur un réseau [INTRU]. L’algorithme utilise l’aléatoire pour générer l’arbre le plus pertinent possible [TREE].
Les systèmes d’exploitation font également usage de nombres aléatoires, notamment pour les tâches d’ordonnancement de processus, mais aussi pour le chiffrement des données ou encore la génération de mots de passes et de jetons de sécurité.
| Champs d’application | Exemples |
| Cryptographie | Génération de mots de passe, clés asymétriques, protocole SSL/TLS … |
| Simulation | Finance, météorologie, estimation d’incertitudes … |
| Algorithmie | Machine learning, algorithmes de tri, parcours de graphes … |
| Jeux vidéos | Comportement, générations de contenu, lootbox … |
| Jeux d’argents en ligne | Paris en ligne, poker, … |
| Systèmes d’exploitation | Chiffrement de données, ordonnancement de processus … |
Ainsi, la génération de nombre aléatoire est cruciale pour de nombreux domaines nécessitant l’intégration d’une composante imprévisible dans leur fonctionnement.
Néanmoins, un ordinateur étant déterministe par nature, il est très difficile de générer informatiquement des nombres qui soient vraiment imprédictibles. Pour obtenir de véritables nombres aléatoires, il faudrait idéalement se tourner vers l’observation de phénomènes physiques.
Cette méthode étant difficile à mettre en place en pratique, on se tourne généralement vers des algorithmes mathématiques visant à simuler l’aléatoire : il s’agit des générateurs de nombres aléatoires, ou PRNG pour Pseudo-Random Number Generator (ou générateur de nombres pseudoaléatoires). Nous décrirons le fonctionnement de ce type de générateur plus tard dans cet article.
Étant donné la criticité des problématiques impliquées, et la complexité du sujet de la génération de nombres aléatoires, des vulnérabilités ont par conséquent été accidentellement introduites et exploitées dans certains de ces mécanismes.
Vulnérabilités liées à des défauts de génération de nombres aléatoires : Un regard sur les failles de sécurité en pratique
Des vulnérabilités liées à des défauts de génération de nombres aléatoires ont été identifiées et exploitées par des acteurs malveillants, cette section décrit trois exemples concrets qui rappellent le besoin crucial de renforcer la sécurité dans ce domaine. En effet, des PRNG insuffisamment robustes ou mal initialisés sont parfois utilisés. Ils peuvent produire des séquences prévisibles, ce qui rend les données générées vulnérables à des attaques.
Avant toute chose, il est important de rappeler que les vulnérabilités connues liées à la génération de nombre aléatoire se rapportent généralement à une de catégories suivantes des CWE du MITRE. En effet, cette liste est suffisamment détaillée et exhaustive pour qualifier avec précision les vulnérabilités connues sur ce type de composant :
CWE-330: Use of Insufficiently Random Values
CWE-331: Insufficient Entropy
CWE-332: Insufficient Entropy in PRNG
CWE-333: Improper Handling of Insufficient Entropy in TRNG
CWE-334: Small Space of Random Values
CWE-335: Incorrect Usage of Seeds in Pseudo-Random Number Generator (PRNG)
CWE-336: Same Seed in Pseudo-Random Number Generator (PRNG)
CWE-337: Predictable Seed in Pseudo-Random Number Generator (PRNG)
CWE-338: Use of Cryptographically Weak Pseudo-Random Number Generator (PRNG)
CWE-339: Small Seed Space in PRNG
CWE-340: Generation of Predictable Numbers or Identifiers
CWE-341: Predictable from Observable State
CWE-342: Predictable Exact Value from Previous Values
CWE-343: Predictable Value Range from Previous Values
Milk Sad : énumération des clés privées générées par un logiciel de wallet de cryptomonnaie
En novembre 2022, puis en juillet 2023, des wallets Bitcoin se sont spontanément retrouvés vidés de leur contenu. Près de 30 bitcoins (soit 900k$) ont été volés. En cause, la vulnérabilité référencée CVE-2023–39910 [CVE-MILKSAD], ou « Milk sad », identifiée par des attaquants sur l’outil de génération de wallet Bitcoin « Libbitcoin Explorer ».
Cet outil utilisait une seed (la valeur d’initialisation du générateur de nombres aléatoire, dont dépend l’entièreté des nombres générés par la suite) de seulement 32 bits pour initialiser le PRNG générant la clé privée du portefeuille bitcoin.
Un total de 2^32, soit 4 294 967 296 clés privées différentes pouvant ainsi être générées [MILKSAD] correspondant au nombre total de seeds différentes pouvant être fournies au PNRG.
Cependant, bien que ce nombre de clés semble élevé, un attaquant créant un programme dédié à l’énumération de ces clés privées pouvait en venir à bout en l’espace de quelques jours. Avec les clés privées ainsi générées, tous les bitcoins associés à ces adresses pouvaient être déplacés sur une adresse contrôlée par l’attaquant.

Cisco utilisait une seed de 32 bits et des valeurs prédictibles pour générer des certificats sur des pare-feu réseau
Dans la même veine, une faille de sécurité liée à un défaut dans l’usage d’un composant générant de l’aléatoire a été identifiée et corrigée dans les composants Cisco FTD et ASA.
Le Cisco FTD (Firepower Threat Defense) est une plateforme de sécurité intégrée qui combine un pare-feu, un système de prévention des intrusions (IPS), et d’autres fonctionnalités de sécurité avancées.
Le Cisco ASA (Adaptive Security Appliance) est un pare-feu de sécurité réseau développé par Cisco, offrant des fonctionnalités de sécurité avancées pour protéger les réseaux et les données des entreprises. Ces composants sont souvent exposés sur Internet et ont un accès au réseau interne des entreprises, ils sont donc des équipements sensibles.
La faille de sécurité CVE-2023-20107 [CVE-CISCO], identifiée dans ces deux composants, résultait d’un problème lié à la génération de nombres aléatoires. Plus précisément, lors de la création de certaines clés cryptographiques dans ces composants, un manque d’entropie de l’état interne du PRNG a été observé.
Ce problème est survenu, car la première seed du générateur de nombres aléatoires n’était longue que de 32 bits. Par la suite, et avant la génération des clés cryptographiques, le temps au démarrage de l’appareil (arrondi à 10ms) était utilisé comme source d’entropie additionnelle. Ces valeurs de temps ne variant que faiblement entre chaque démarrage, et les 32 bits de la seed pouvant être énumérés, tous les nombres et les clés pouvant être générés subséquemment l’étaient aussi [CVE-CISCO-SSTIC].
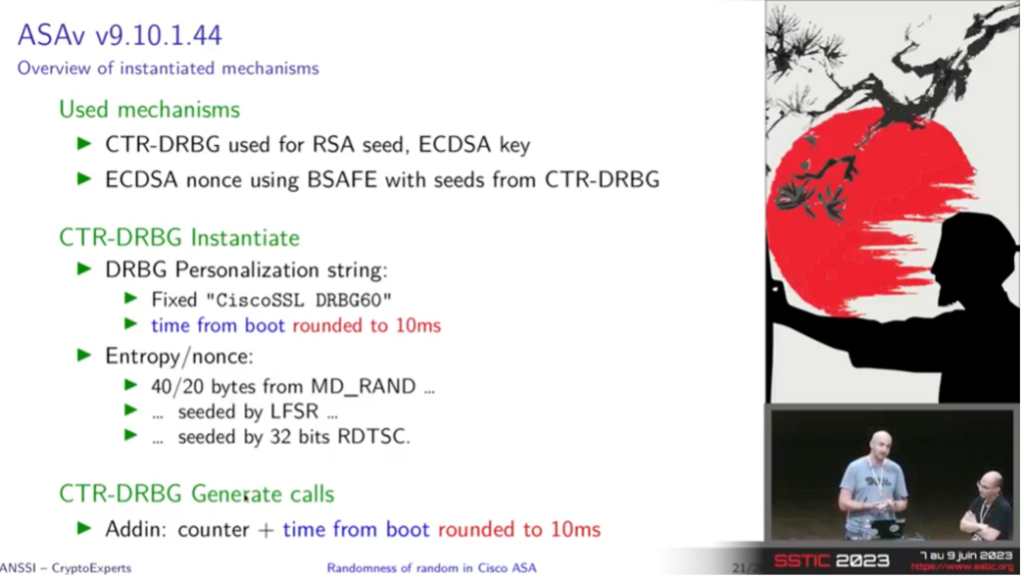
Cette vulnérabilité se rapporte à la faiblesse « CWE-332: Insufficient Entropy in PRNG », causée par les faiblesses « CWE-337: Predictable Seed in Pseudo-Random Number Generator (PRNG) » et « CWE-339: Small Seed Space in PRNG ».
Le PID, une si mauvaise seed ? Oui, comme l’a constaté OpenSSL
Nous ne pouvions rédiger cet article sans rappeler la fameuse vulnérabilité d’OpenSSL découverte en mai 2008 par les équipes de Debian. Cette vulnérabilité, référencée CVE-2008-0166 [CVE-OPENSSL] affecte les certificats générés à l’aide d’OpenSSL entre septembre 2006 (date à laquelle cette faille a été introduite) et mai 2008 (date de sa correction). La régénération de tous ces certificats a été nécessaire, car leurs clés cryptographiques pouvaient potentiellement être regénérées par un attaquant, lui permettant ainsi de mener des attaques de type MITM (Man-In-The-Middle) sur des flux pourtant sécurisés par le protocole SSL / TLS ou SSH.
La vulnérabilité résidait dans l’utilisation exclusive de l’identifiant de processus (PID) au lieu de combiner diverses sources d’entropie pour créer la seed initiale du PRNG. Cela signifiait qu’il n’y avait que 32 768 valeurs possibles de graine pour toutes les opérations du générateur de nombres pseudoaléatoires.
Un attaquant avait donc la possibilité, comme illustré dans cet exemple [DEBG], de générer l’ensemble des clés DSA-1024 et RSA-2048 en quelques heures. Cette démarche visait, entre autres, à découvrir la clé privée utilisée par un serveur SSH , permettant à un attaquant de lire les données échangées avec l’interface d’administration SSH vulnérable.
Cette vulnérabilité se rapporte à la faiblesse « CWE-337: Predictable Seed in Pseudo-Random Number Generator (PRNG) ».
Ce que ces cas nous apprennent
La possibilité pour des attaquants d’exploiter des défauts d’implémentations et de configuration dans des algorithmes de génération d’aléatoire ainsi que leur usage répandu nécessite d’être capable de contrôler l’imprédictibilité des nombres générés.
Cela doit être réalisé via deux approches différentes :
- via l’analyse de l’implémentation ;
- par des tests statistiques sur la sortie de ces générateurs.
Tester les outils de test : une histoire de tests ?
Nous faisons maintenant un état des lieux des outils les plus connus pour réaliser des tests sur des suites de nombres aléatoires, ce qui permet de qualifier l’imprédictibilité des nombres générés.
Parmi les différents outils disponibles, nous en avons relevé trois, généralement reconnus comme étant des références :
- Diehard [DIE]
- NIST Statistical Test Suite [NIST-TOOL]
- TestU01 [TU01-LIB]
Notre objectif est de présenter à la fois la complétude des tests statistiques des outils mais aussi (et surtout) d’évoquer leur facilité d’installation et de prise en main dans des cas pratiques, pour un utilisateur occasionnel.
DieHard et DieHarder
Diehard est une suite de tests publiée en 1995 par le mathématicien George Marsaglia sous la forme d’un CDROM [DIE]. Elle est écrite en C et en Fortran. Elle permet d’exécuter 16 tests statistiques sur des séries de bits issues de « générateurs de nombres aléatoires ».
Il s’agit de la suite de tests pour générateurs de nombres aléatoires la plus connue. Il a influencé d’autres outils populaires, notamment NIST Statistical Test Suite, qui a repris l’un de ses tests (Binary Matrix Rank Test) directement de la suite Diehard.
En 2003, un nouvel outil nommé Dieharder [DIER] fut développé. L’objectif de ce dernier était d’assembler en un seul outil les tests associés au NIST Statistical Tests Suite et à Diehard. Il s’agit à l’heure actuelle de l’implémentation de Diehard la plus simple d’accès. Nous nous concentrerons donc sur celle-ci pour la suite de l’article.
La capture suivante montre un exemple d’utilisation de l’outil Dieharder. Cette dernière applique un « run test » (indiqué par le paramètre « -d 15 ») sur une série de bits issues de /dev/urandom (indiqué par le paramètre « -g 501 »). Le paramètre « -t » permet de renseigner la taille de l’échantillon (soit 1000000).
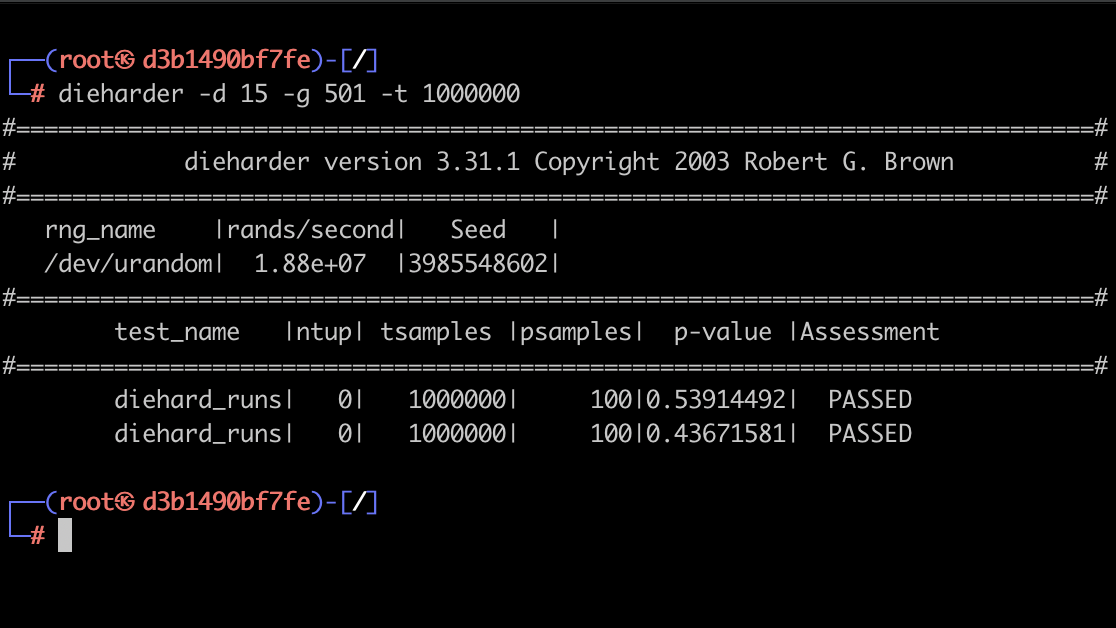
Les résultats montrent l’application d’une série de deux tests. Une p-value inférieur à 0.995 et supérieure à 0.005 est indiquée pour chacun des tests montrant le succès de ces derniers.
Malgré l’utilisation de code très peu intuitif pour renseigner les paramètres, Dieharder a été l’un des outils les plus simples à tester parmi ceux que nous avons évoqués. La première utilisation est complexe, mais un habitué des outils open source intègrera rapidement la logique de celui-ci.
Nous déplorons malheureusement le faible niveau de documentation de l’outil. Une page HTML résume de façon partielle les fonctionnalités de celui-ci. Certains paramètres restent peu compréhensibles et ne semblent pas être approfondis au-delà de ce qu’indique l’aide de la commande.
NIST Statistical Test Suite (STS)
Le NIST (National Institute of Standards and Technology) est un organisme public états-unien, ayant notamment pour rôle de gérer différents standards au sein de l’industrie. Une partie de leurs domaines de compétences inclut la sécurité informatique et la cryptographe. Ces derniers définissent des standards concernant la sécurité des générateurs aléatoires, servant de références au-delà des frontières américaines.
Afin de tester des générateurs de nombres aléatoires à des fins de certification, le NIST a publié en 2008 une suite écrite sous la forme d’une commande en langage C. De même que pour Diehard, l’outil prend en entrée des séries de bits. Il applique notamment une quinzaine de tests, décrit dans un document de référence [NIST-TEST]. L’outil a été révisé en 2010, il s’agit de sa version actuelle.
La suite peut être téléchargée via le site Web du NIST [NIST-TOOL].
La capture suivante montre un exemple d’utilisation de l’outil du NIST. L’exécutable à compiler soi-même se note « assess » et prend en paramètre la taille des échantillons à analyser (ici 100000). La configuration des tests se fait via des interactions successives avec l’utilisateur (via stdin).
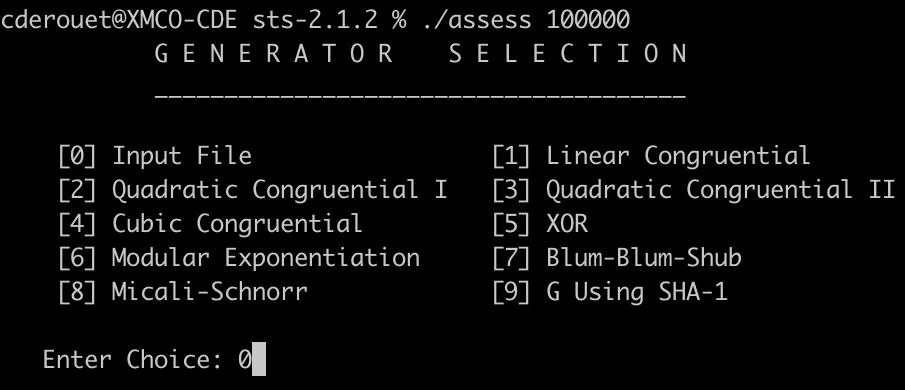
Cette façon d’interagir avec l’outil est peu confortable pour les utilisateurs habitués à utiliser un terminal de commande. Elle empêche l’autocomplétion du nom des fichiers et empêche de scripter la réalisation de test à des fins d’automatisation.
Le fichier suivant montre le résultat du « serial test » appliqué avec les paramètres par défaut sur l’échantillon de démonstration « data.pi ».
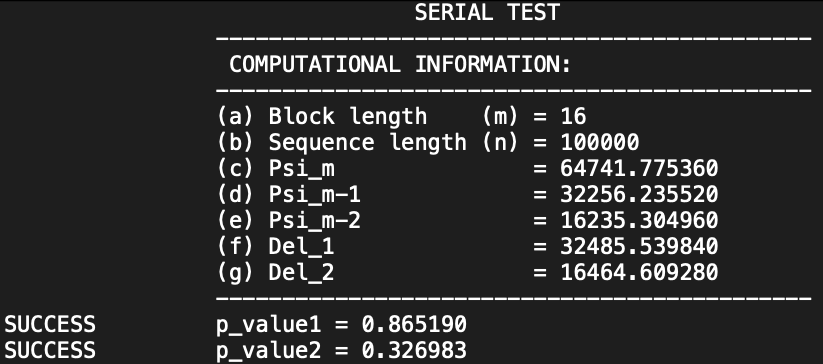
L’interprétation montre les p-values issues d’une série de deux tests. Les deux p-values ont une valeur supérieure à 0.01, indiquant le succès du test (comme indiqué sur la gauche de la capture). Ici, la p-value représente la probabilité d’obtenir les résultats observés si le générateur était parfaitement aléatoire (des définitions précises des termes statistiques seront données dans notre prochain article).
La série de tests effectués a permis de constater les défauts suivants :
- Aucune documentation officielle permettant de savoir comment utiliser l’outil ne semble avoir été diffusée ; si cette dernière existe, l’emplacement est peu évident.
- L’outil est instable et a cessé de fonctionner plusieurs fois lors de l’utilisation.
On remarque cependant les points positifs suivants :
- La compilation de l’outil n’a pas présenté de difficulté particulière malgré l’absence de documentation.
- Les tests réalisés sont extrêmement bien documentés d’un point de vue mathématique (malgré l’absence apparente de documentation technique) [NIST-DOC].
TestU01
Le dernier outil évoqué sera TestU01. Il a été développé par Pierre L’Ecuyer et Richard Simard en 2007, chercheurs à l’Université de Montréal. Il s’agit de la suite de test la plus récente évoquée dans cet article.
Contrairement aux précédentes suites de tests, celle-ci ne se présente pas comme une commande prête à l’emploi, mais plutôt comme une bibliothèque de fonctions intégrables dans un programme en langage C. Il faut donc programmer et compiler son propre code source en utilisant les fonctions fournies pour réaliser ces tests.
Cette différence s’explique par une volonté assumée des créateurs de la suite de proposer un outil plus poussé et plus configurable que « Diehard » et que la « NIST Statistical Test Suite » (tels que décrit dans ce papier [TU01-PAPER]). Un utilisateur peut ainsi créer ses propres batteries de tests et les exécuter en série.
La bibliothèque contient 4 types de composant :
- Des tests statistiques individuels pour les générateurs de nombre aléatoire (le coeur de métier de l’outil) ;
- Des batteries de tests prédéfinies (il s’agit de d’une liste de tests individuels regroupés et exécutés en série sur des données) ;
- Des générateurs de nombre pseudo aléatoires prédéfinis ;
- Des outils de test pour les familles de générateurs (qui permettent notamment de vérifier à partir de quelle taille d’échantillon l’outil échoue de façon systématique).
Contrairement aux deux précédentes suites, l’outil est à la fois capable de tester des séquences de bits et des séries de nombres réels situés entre 0 et 1.
La bibliothèque logicielle peut être récupérée via un dépôt Github publié par l’éditeur [TU01-LIB]. Un guide utilisateur de l’outil [TU01-DOC] a par ailleurs été publié.
La capture d’écran suivante montre la compilation du code d’exemple « bat1.c » et l’exécution de ce dernier. Il applique une batterie de tests sur un générateur de nombre aléatoire de type LGC. Les tests suivants sont inclus dans la batterie :
- smarsa_BirthdaySpacings ;
- sknuth_Collision ;
- sknuth_Gap ;
- sknuth_SimpPoker ;
- sknuth_CouponCollector
- sknuth_MaxOft ;
- svaria_WeightDistrib ;
- smarsa_MatrixRank ;
- sstring_HammingIndep ;
- swalk_RandomWalk1.
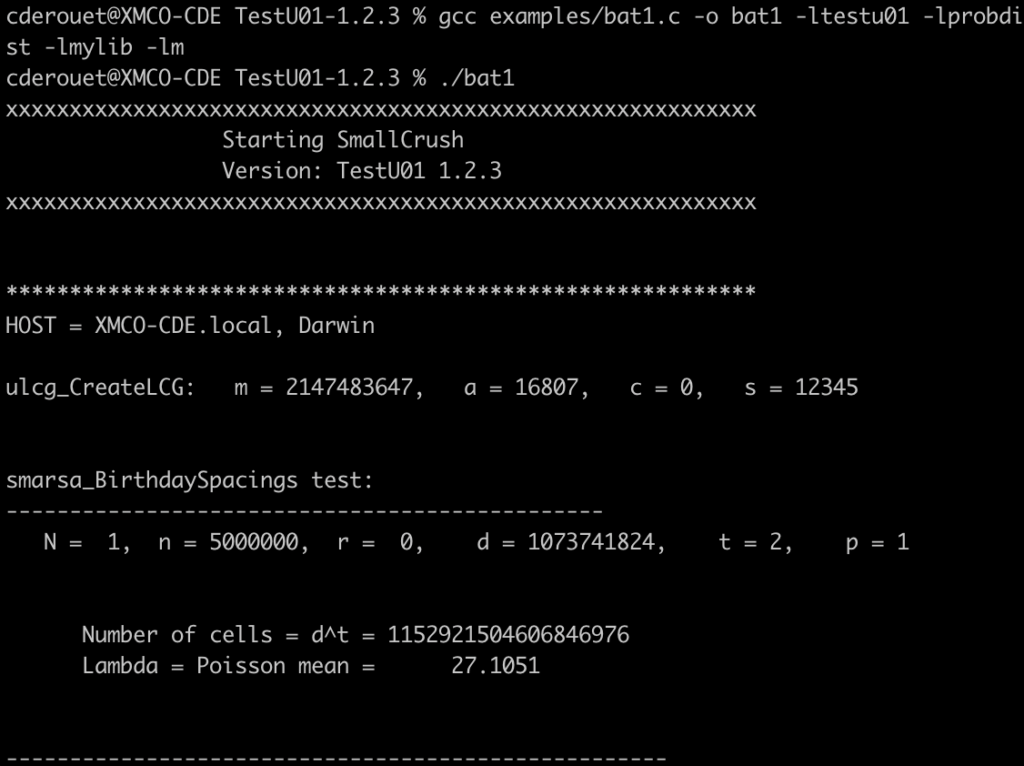
La capture suivante montre la synthèse des tests de l’outil.
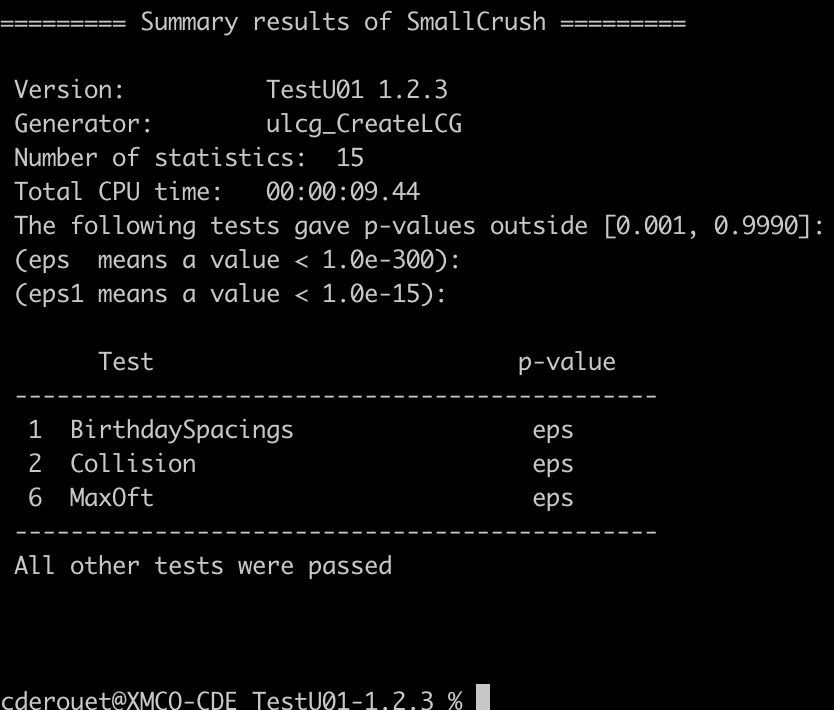
La synthèse montre que trois tests ont échoué. L’outil attend une p-value comprise dans l’intervalle [0.001, 0.999].
Bien que les états des tests soient affichés au fur et à mesure durant l’exécution, ce résumé est assez faible en information. Les autres outils présentés montrent des tableaux de résultat indiquant les p-values en plus de les qualifiés. Ces dernières ne sont pas présentées de façon précise ici. De plus, seuls les tests échoués sont explicitement présentés.
Toutefois, si ce point est bloquant, la souplesse apportée par le fait de programmer soi-même son propre exécutable peut permettre de développer au cas échéant un autre format de sortie (quitte à devoir réimplémenter quelques composants de l’outil).
Notons également que la documentation de la bibliothèque ne sera pas forcément confortable pour un développeur. Il s’agit d’un PDF de taille conséquente et sans sommaire cliquable permettant d’accéder rapidement à une section précise.
Tableau comparatif des tests statistiques implémentés au sein des outils Dieharder, NIST Test Suite et TestU01
Dans cette section, nous comparons les tests statistiques implémentés dans les différents outils : Dieharder [DIER], NIST Test Suite [NIST-TEST] et TestU01 [TU01-DOC].
| Diehard | NIST Test Suite | Dieharder | TestU01 | |
| Monobit (Chi2) | x | x | x | x |
| Frequency in block | x | x | x | x |
| Run Test | x | x | x | x |
| Longest run of Ones | x | x | x | |
| Binary Rank | x | x | x | x |
| DFT | x | x | x | |
| Non-overlapping template matching | x | x | x | x |
| Overlapping template matching | x | x | x | |
| Maurer test | x | x | x | |
| Lempel-Ziv | x | x | x | |
| Linear Complexity | x | x | x | |
| Serial | x | x | x | |
| Approximate entropy | x | x | x | |
| Cumulative Sums | x | x | x | |
| Random excursions | x | x | ||
| Brithday Spacing | x | x | x | |
| 5-Permutation | x | x | ||
| OPSO/OQSO | x | x | x | |
| DNA | x | x | x | |
| Parking Lot | x | x | ||
| Minimum Distance | x | x | x | |
| 3-D Spheres | x | x | ||
| Craps | x | x | ||
| Squeeze | x | x | x | |
| Autres tests de « Crush » | x (plusieurs tests) | |||
| Autres tests de « BigCrush » | x (plusieurs tests) |
Il est important de noter que TestU01 implémente trois batteries de tests : SmallCrush, Crush et BigCrush. Le nombre de tests de ces batteries étant très important, ils ne sont pas tous listés dans ce tableau.
D’un point de vue purement statistique, TestU01 est la suite de tests la plus complète.
Tableau d’évaluation d’usage des outils Dieharder, NIST Test Suite et TestU01
Le tableau ci-dessous compare les solutions évoquées précédemment en s’appuyant sur une série de critères et de caractéristiques choisis par des auditeurs. L’objectif de cette comparaison est d’aider à l’identification des outils les plus pertinents en fonction des besoins des utilisateurs.
Cette qualification reste une vision [subjective] des consultants XMCO après quelques heures d’usage / de recherche de chacun des outils, dans le cadre d’audits techniques liés à l’aléatoire.
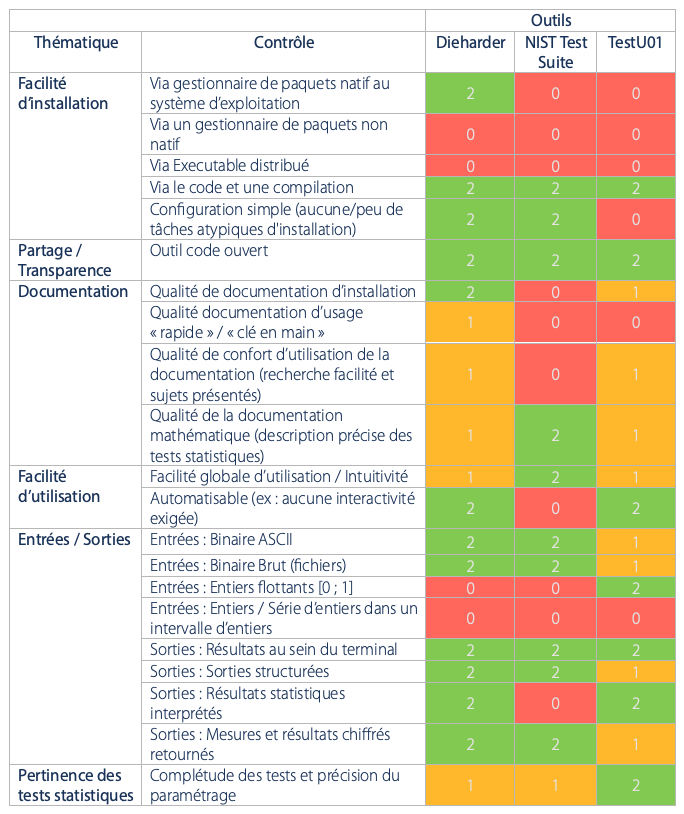
Légende :
Rouge (0) : Inexistant / Difficile à identifier / Complexe
Orange (1) : Partiellement traité
Vert (2) : Complet / Suffisant
Synthèse et perspectives
Dans cet article, nous avons pu constater que :
- La génération de nombres aléatoires est largement utilisée dans notre quotidien
- La mauvaise conception et implémentation peut mener à des défauts de sécurité critiques.
Ainsi, il est nécessaire de faire auditer et valider l’implémentation des générateurs de nombres aléatoires, et leurs mécanismes d’initialisation. Des tests statistiques doivent également être effectués sur la sortie des générateurs aléatoires afin de s’assurer de leur qualité.
Plusieurs outils open-source existent et permettent de réaliser ces tests :
- Dieharder
- NIST test Suite
- TestU01
Néanmoins ces outils ne sont plus maintenus, parfois difficiles à installer et/ou à utiliser et peuvent demander des compétences statistiques avancées.
Dans notre prochain article, nous présenterons un outil développé par l’équipe XMCO ayant pour vocation d’être rendu open-source permettant de tester simplement des générateurs aléatoires.
Antoine R., Clément D. et Nicolas G.
Références
[ET2] https://ressources.anj.fr/regulation/homologation_logiciel/et2.pdf
[MC] https://en.wikipedia.org/wiki/Monte_Carlo_method
[INTRU] http://www.iro.umontreal.ca/~simardr/testu01/guideshorttestu01.pdf
[TREE] https://en.wikipedia.org/wiki/Decision_tree
[CVE-OPENSSL] https://cve.mitre.org/cgi-bin/cvename.cgi?name=cve-2008-0166
[CVE-CISCO-SSTIC] https://www.sstic.org/2023/presentation/randomness_of_random_in_cisco_asa/
[MILKSAD] https://milksad.info
[CVE-MILKSAD] https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2023-39910
[DEBG] https://github.com/g0tmi1k/debian-ssh
[DIER] https://webhome.phy.duke.edu/~rgb/General/dieharder.php
[DIE] http://www.stat.fsu.edu/pub/diehard/
[NIST-TOOL] https://csrc.nist.gov/projects/random-bit-generation/documentation-and-software
[NIST-DOC] https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-22r1a.pdf
[TU01-DOC] http://www.iro.umontreal.ca/~simardr/testu01/guideshorttestu01.pdf
[TU01-PAPER] https://www.iro.umontreal.ca/~lecuyer/myftp/papers/testu01.pdf


